【答案】(1)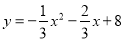 �;(2)(﹣1,
�;(2)(﹣1, 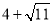 )或(﹣1�����,
)或(﹣1�����,  )����;(3)F(﹣1,4)或(﹣1����,﹣4)或(﹣1,12).
)����;(3)F(﹣1,4)或(﹣1����,﹣4)或(﹣1,12).
【解析】試題分析:(1)把點A�����,B的坐標代入拋物線解析式����,解方程組即可.
(2)作DM⊥拋物線的對稱軸于點M,設G點的坐標為(﹣1,n)����,由翻折的性質,得到BD=DG����;然后求出點D、點M的坐標�����,以及BC�����、BD的值����;在Rt△GDM中,由勾股定理��,求出n的值�,即可求出G點的坐標.
(3)分三種情況討論:①當CD∥EF,且點E在x軸的正半軸時��;②當CD∥EF,且點E在x軸的負半軸時�;③當CE∥DF時;然后根據平行四邊形的性質����,求出點F的坐標各是多少即可.
試題解析:(1)∵拋物線 經過點A(﹣6��,0)�,B(4,0)��,∴
經過點A(﹣6��,0)�,B(4,0)��,∴ ����,解得
����,解得 ,∴拋物線的解析式是:
,∴拋物線的解析式是: 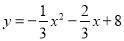 �;
�;
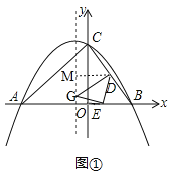
(2)如圖①,作DM⊥拋物線的對稱軸于點M����,
 ,
,
設G點的坐標為(﹣1�,n),由翻折的性質��,可得BD=DG,∵B(4��,0)����,C(0,8)��,點D為BC的中點����,∴點D的坐標是(2,4)����,∴點M的坐標是(﹣1,4)����,DM=2﹣(﹣1)=3,∵B(4�����,0)�����,C(0�����,8)�����,∴BC=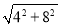 =
=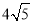 �,∴BD=
�,∴BD= �,在Rt△GDM中,32+(4﹣n)2=20����,解得n=
�,在Rt△GDM中,32+(4﹣n)2=20����,解得n=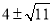 ��,∴G點的坐標為(﹣1�,
��,∴G點的坐標為(﹣1�, 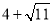 )或(﹣1��,
)或(﹣1��, 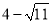 )��;
)��;
(3)拋物線 的對稱軸上存在點F�����,使得以C��、D��、E��、F為頂點的四邊形為平行四邊形.
的對稱軸上存在點F�����,使得以C��、D��、E��、F為頂點的四邊形為平行四邊形.
①當CD∥EF�,且點E在x軸的正半軸時�,如圖②�,
 ,
,
由(2)����,可得點D的坐標是(2,4)��,設點E的坐標是(c�����,0),點F的坐標是(﹣1����,d),則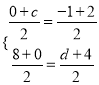 ����,解得
����,解得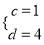 ,∴點F的坐標是(﹣1��,4)����,點C的坐標是(1��,0)��;
,∴點F的坐標是(﹣1��,4)����,點C的坐標是(1��,0)��;
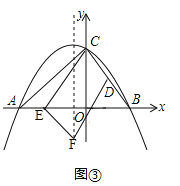
②當CD∥EF�����,且點E在x軸的負半軸時����,如圖③����,
 ��,
��,
由(2)�,可得點D的坐標是(2,4)�����,設點E的坐標是(c����,0),點F的坐標是(﹣1��,d)��,則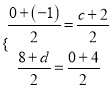 �,解得
�,解得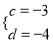 ,∴點F的坐標是(﹣1��,﹣4)�,點C的坐標是(﹣3,0);
,∴點F的坐標是(﹣1��,﹣4)�,點C的坐標是(﹣3,0);
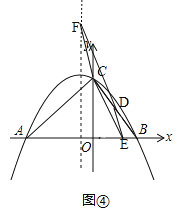
③當CE∥DF時�,如圖④,
 ����,
����,
由(2),可得點D的坐標是(2����,4),設點E的坐標是(c�,0),點F的坐標是(﹣1�����,d)��,
則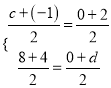 ��,解得:
��,解得:  ����,∴點F的坐標是(﹣1��,12),點C的坐標是(3�,0);
����,∴點F的坐標是(﹣1��,12),點C的坐標是(3�,0);
綜上����,可得拋物線 的對稱軸上存在點F,使得以C����、D、E�����、F為頂點的四邊形為平行四邊形��,點F的坐標是(﹣1����,4)、(﹣1�����,﹣4)或(﹣1��,12).
的對稱軸上存在點F,使得以C����、D、E�����、F為頂點的四邊形為平行四邊形��,點F的坐標是(﹣1����,4)、(﹣1�����,﹣4)或(﹣1��,12).