
Ó}ńŅŃ–ĪŪ(įŁņ®īūįłļÕĹ‚őŲ)
| x2 |
| 4 |
| y2 |
| 5 |
| x2 |
| a2 |
| y2 |
| b2 |
| 2b2 |
| a |
| x2 |
| a2 |
| y2 |
| b2 |
| 2b2 |
| a |
| x2 |
| 4 |
| y2 |
| 5 |
| ¶– |
| 4 |
| 2 |
| x |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
“—÷™ļĮĒĶ(sh®ī)f(x)=ax- -3ln x,∆š÷–aěť≥£ĒĶ(sh®ī).
-3ln x,∆š÷–aěť≥£ĒĶ(sh®ī).
(1)ģĒ(d®°ng)ļĮĒĶ(sh®ī)f(x)ĶńąDŌů‘ŕŁc ŐéĶń«–ĺÄĶń–Ī¬ ěť1ēr,«ůļĮĒĶ(sh®ī)f(x)‘ŕ
ŐéĶń«–ĺÄĶń–Ī¬ ěť1ēr,«ůļĮĒĶ(sh®ī)f(x)‘ŕ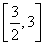 …ŌĶń◊Ó–°÷Ķ;
…ŌĶń◊Ó–°÷Ķ;
(2)»ŰļĮĒĶ(sh®ī)f(x)‘ŕÖ^(q®Ī)ťg(0,+°ř)…Ōľ»”–ėOīů÷Ķ”÷”–ėO–°÷Ķ,«ůaĶń»°÷Ķ∑∂áķ;
(3)‘ŕ(1)ĶńólľĢŌ¬,Ŗ^ŁcP(1,-4)◊ųļĮĒĶ(sh®ī)F(x)=x2[f(x)+3lnx-3]ąDŌůĶń«–ĺÄ,‘áÜĖŖ@ė”Ķń«–ĺÄ”–é◊ól?≤Ę«ů≥ŲŖ@–©«–ĺÄ∑Ĺ≥Ő.
įŔ∂»÷¬–Ň - ĺöŃē(x®™)É‘Ń–ĪŪ - ‘áÓ}Ń–ĪŪ
ļĢĪĪ °Ľ•¬ď(li®Ęn)ĺW(w®£ng)Ŗ`∑®ļÕ≤ĽŃľ–ŇŌĘŇeąů∆ĹŇ_ | ĺW(w®£ng)…Ō”–ļ¶–ŇŌĘŇeąůĆ£Ö^(q®Ī) | Žä–Ň‘pÚ_ŇeąůĆ£Ö^(q®Ī) | …śöv ∑Őďüo÷ųŃx”–ļ¶–ŇŌĘŇeąůĆ£Ö^(q®Ī) | …ś∆ů«÷ôŗ(qu®Ęn)ŇeąůĆ£Ö^(q®Ī)
Ŗ`∑®ļÕ≤ĽŃľ–ŇŌĘŇeąůŽä‘í£ļ027-86699610 Ňeąůŗ]Ōš£ļ58377363@163.com