
| lim |
| Ī„xĪ·0 |
| f(x0+Ī„x)-f(x0-3Ī„x) |
| 2Ī„x |
| lim |
| Ī„xĪ·0 |
| f(x0+Ī„x)-f(x0) |
| Ī„x |
| lim |
| Ī„xĪ·0 |
| f(x0+Ī„x)-f(x0-3Ī„x) |
| 2Ī„x |
| lim |
| Ī„xĪ·0 |
| f(x0+Ī„x)-f(x0) |
| Ī„x |
| lim |
| Ī„xĪ·0 |
| f(x0+Ī„x)-f(x0) |
| Ī„x |
| lim |
| Ī„xĪ·0 |
| f(x0+Ī„x)-f(x0-3Ī„x) |
| 2Ī„x |
| lim |
| Ī„xĪ·0 |
| f(x0+Ī„x)-f(x0-3Ī„x) |
| 4Ī„x |
| lim |
| Ī„xĪ·0 |
| f(x0+Ī„x)-f(x0) |
| Ī„x |



| ─Ļ╝ē | Ė▀ųąšn│╠ | ─Ļ╝ē | │§ųąšn│╠ |
| Ė▀ę╗ | Ė▀ę╗├Ō┘M(f©©i)šn│╠═Ų╦]ŻĪ | │§ę╗ | │§ę╗├Ō┘M(f©©i)šn│╠═Ų╦]ŻĪ |
| Ė▀Č■ | Ė▀Č■├Ō┘M(f©©i)šn│╠═Ų╦]ŻĪ | │§Č■ | │§Č■├Ō┘M(f©©i)šn│╠═Ų╦]ŻĪ |
| Ė▀╚² | Ė▀╚²├Ō┘M(f©©i)šn│╠═Ų╦]ŻĪ | │§╚² | │§╚²├Ō┘M(f©©i)šn│╠═Ų╦]ŻĪ |
┐Ų─┐Ż║Ė▀ųąöĄ(sh©┤)īW(xu©”) üĒį┤Ż║ Ņ}ą═Ż║
| lim |
| Ī„xĪ·0 |
| f(x0+2Ī„x)-f(x0) |
| 3Ī„x |
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║Ė▀ųąöĄ(sh©┤)īW(xu©”) üĒį┤Ż║ Ņ}ą═Ż║
| a |
| 3 |
| b |
| ”ą |
| 2 |
| a |
| b |
| ”ą |
| 2 |
| ”ą |
| 2 |
| 14 |
| 5 |
| ”ą |
| 4 |
| ”ą |
| 2 |
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║Ė▀ųąöĄ(sh©┤)īW(xu©”) üĒį┤Ż║ Ņ}ą═Ż║å╬▀xŅ}
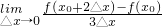 Ą─ųĄ╩Ū
Ą─ųĄ╩Ū

▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
┐Ų─┐Ż║Ė▀ųąöĄ(sh©┤)īW(xu©”) üĒį┤Ż║▓╗įö Ņ}ą═Ż║å╬▀xŅ}
| lim |
| Ī„xĪ·0 |
| f(x0+2Ī„x)-f(x0) |
| 3Ī„x |
| AŻ«3 | BŻ«2 | CŻ«
| DŻ«
|
▓ķ┐┤┤░Ė║═ĮŌ╬÷>>
░┘Č╚ų┬ą┼ - ŠÜ┴Ģ(x©¬)āį┴ą▒Ē - įćŅ}┴ą▒Ē
║■▒▒╩Ī╗ź┬ō(li©ón)ŠW(w©Żng)▀`Ę©║═▓╗┴╝ą┼Žó┼eł¾(b©żo)ŲĮ┼_ | ŠW(w©Żng)╔Žėą║”ą┼Žó┼eł¾(b©żo)īŻģ^(q©▒) | ļŖą┼įp“_┼eł¾(b©żo)īŻģ^(q©▒) | ╔µÜv╩Ę╠ō¤oų„┴xėą║”ą┼Žó┼eł¾(b©żo)īŻģ^(q©▒) | ╔µŲ¾ŪųÖÓ(qu©ón)┼eł¾(b©żo)īŻģ^(q©▒)
▀`Ę©║═▓╗┴╝ą┼Žó┼eł¾(b©żo)ļŖįÆŻ║027-86699610 ┼eł¾(b©żo)Ó]ŽõŻ║58377363@163.com